听音室的最佳三维尺寸

behringer

    室内共振模式虽然会在频率响应上产生些峰值和谷值，但却可以通过挑选房间的长、宽、高的合理比值来使共振模式在低频端分布能够更为均匀些而将这些峰值和谷值减为最小。现在便以大小完全相同，但房间的长、高、宽比不同的两间房间为例，看看室内共振模式的不同影响。

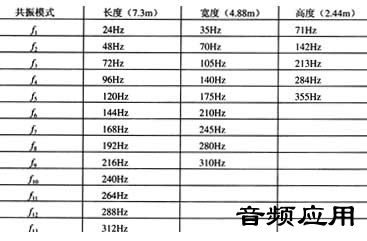
     第一间听音室的长、高、宽尺寸比例不大好。其长度为7.3m，宽度为4.88m，高度为2.44m。因此，可分别计算出在长、高、宽上的室内共振模式如表1所示。
; ^* O& t! ~7 n  n- U- w0 [3 z7 A
1 l- I; |  Q( X% t1 a' S4 l! E) Q

0 S" D' e/ m: {6 {0 o
& l+ Q" R8 Q# d8 T
  @: H) ^! }: v0 u9 A- ]
. p+ t' d7 p* c9 t: ]表1 第一间房间内的共振模式


    注意长度上的第三共振模式（f3）为72Hz，跟宽度上的第二共振模式（f2）的70 Hz以及高度上的第一共振模式（f1）的71Hz基本上重合，这三个共振模式的重合，便会在频率响应的70Hz处产生一个极大的峰值。这种极令人讨厌的情况还分别在140Hz，213Hz以及284Hz时出现。这些共振模式之所以会重合的原因是：听音室在长度、宽度和高度上的比值刚好为倍数的关系。实际上，长、宽、高的三个共振模式中，在频率70.6Hz，141.2Hz等的频率上是完全重合的。由于四舍五入的关系，才将它们稍微拉开了点了而便于观看（图1便是这些共振模式同频率的关系图）。


1 O  N1 k0 N# R5 I, l  t$ ^
) }. _0 R" a+ B$ ]* Q. G, ~

4 T0 R) k6 O$ Q* ^图1 共振模式图
7 s" }  t2 L/ s3 J4 i( T6 G
# s( q+ ]8 v1 L0 V3 X
在105Hz到140Hz之间并无共振模式出现，因此在140Hz的叠积便更易于听出来。结果便会在重放时听到一个相当响亮、过重和声染色严重的低音。

    由图1见，共振模式比较靠得近，因而留下的间隔很大。共振模式之间的“空洞”的危害同那些重合的共振模式的危害是一样的。它们将会使相邻近的共振模式听得更为明显。
7 J1 C( Q8 g9 L' q
4 h' c5 Q* H, U* G    现在再来看看长、高、宽三维尺寸较好的第二间听音室的情况。这间听音室的空间和第一间听音室差不多。但房间的宽度、高度和长度的比例好些。其长度、宽度、高度的尺寸分别为6.4m，4.27m，3.05m。对第一尺寸所计算出的室内共振模式如表2所示。
0 Z' p1 C0 ?- r; H6 J# `0 B
6 |( g% J3 j1 l8 _, Y7 m( `
8 {# L. U( \% C+ t- O1 H


表2 第二间房间内的共振模式

1 r9 v6 q* `" |2 B3 Q5 {
; D0 k& H& `: W! d根据此表所列的数据而绘出的共振模式图如图2所示。



$ }% S: V+ c4 _" n- Z

图2 房间比例尺寸好时的共振模式图
( C! }/ O7 Y3 _0 _+ R

    比较图1和图2，第二间听音室内的共振模式分布得更为均匀些。虽然还是有共振模式的重合，但已不再像第一间听音室那么严重。第二间听音室的低频响应便更平坦些，声染色也少了点，低音也比第一间听音室的更紧凑结实和更有力些。注意房间大些时，固有的共振模式也自然会多些，因此，如果房间的比例尺寸也好时，分布便会更为均匀。房间越小，室内共振模式的分布便越差。
" [" d4 U8 r$ R4 N1 h& L1 k! k
/ v" r: n9 n' X! Y    倾斜的天花板将会使高度上的共振模式也跟着起些变化，因而不会再像普通房间那样让共振模式出现在与之相同的频率上，而是拉开了一点。如果天花的低端为2.4m，高端为3.6m，则在计算时可取高度的平均值3m。倾斜的天花板虽然不能消除共振模式，但却可以使共分布得到改善。同样，倾余的墙壁也能够让共振模式跟着倾斜，但却不能消除共振模式。

+ h" e8 G4 \! ~3 H7 M! x    如果能够避免使用正方形或立方形的房间来作为听音室，则室内共振模式的影响便不会显得那么明显。也就是说，尽量不用宽度和高度相同或是宽度与长度相等或是长度与高度一样的房间。当然，三边尺寸相等或是长边与短边成倍数关系的房间也不宜使用。如果天花板高2.4m，便应尽量避免再有2.4m，4.8m和7.2m的宽边或长边。注意共振模式是始终存在的。三边比值好些的房间只不过能够让共振模式分布得均匀些而不能阻止共振模式的重合。表3是根据美国声学家M.M.Louden（劳登）的计算而按照好坏程度列出的房间的最佳比值。
6 i; k+ D2 d  q% `) s
9 \  T. t/ v1 X& U6 Y; E
7 o$ s; T" \8 F3 R+ ^

6 w8 D5 ^8 s+ }2 C
表3 听音室长、宽、高的最佳比值表
4 L: r. g2 V" s6 L  ^
; K3 w( m5 h) Z1 r8 {% d! W
) H0 ?' I) Y7 n, b$ ]- z% F注：表中的X可以是房间的长度，而Y可为宽度，反之也可。


) C: Q* W8 v6 S. C" q     根据此表，对于天花板高为2.64m的房间，理想的长度和宽度尺寸便分别应为2.64×1.9=4.94（m）和2.64×1.4=3.64（m）。而对天花板高3.8m的房间，最佳的长度和宽度则分别应为7.3m和5.3m。注意，虽然对于二个不同高度的天花板可以计算出不同的数值。但长、宽、高的比值仍是相同的。正是由这些比值去确定室内共振模式将会如何地分布。
6 R- X" B( [6 v% b, W! X7 u! N0 z7 C
) f2 I7 L' w4 c: ~1 {    此外，三维尺寸比值好的大房间便比同样比值的小房间的音响效果要好些。在大房间内会产生更多的共振模式，因之在频率上会靠得更近些，分布自然会均匀些。但应记住，好的比值并不能阻止共振的发生，只不过能让共振在音频频带内分布得均匀些。好的比值可以防止共振模式的重合，并消除影响更严重的共振模式之间的那些间隔。
: v: c% t# s7 t. |% t# b$ |
# O! R( _& j0 e3 k- f+ F' V    如果没有条件去挑选一间各边比例尺寸适当的房间。便可以按照本章后边介绍的方法进行室内声学处理，以尽量减少室内共振模式的影响。

    用于计算室内共模式的软件目前已不那么贵了。例如，在给出房间的各边尺寸后，便可用RPG的室内最佳化软件来进行全面的仿真计算。求出推荐的音箱的摆放位置和聆听参考位置。
; }3 A. T* C2 o. T, g& @
    以上对室内共振模式的讨论还是大大经过简化后的情况。即在两平面之间的轴上模式（axial mode）。此外，还有两对平面（四面）的切面模式（tangential mode）和三对平面（六面）的斜面模式（oblique mode）。关于这些问题的讨论可参看专门的声学书籍。

luyinliu

点赞了，好文章，不错啊，可以收藏学习了啊！~